Would you bag your machine learning models or rather stack them?

Data Science is such a field that we can interpret it as a domain in itself and a domain enabler. The phrase ‘Domain enabler’ just means that we can use data science as a generalized light source in any domain like IT, mechanical, medical, manufacturing, aeronautical....etc to shed some light on what the future of the respective domains/organizations depend on. Of course, I would be lying if I just said that the above interpretation is all that you need to understand the phrase ‘Domain enabler’. The purpose of this article is neither to interpret the phrase nor to understand the basics of data science and machine learning.
On the contrary, I assume that the reader has a very good or sufficient understanding of the Data science domain and machine learning algorithms. Each domain would possibly shoot a different requirement or a problem statement and hence a possibly different generalization of prediction, a different improvisation analogy with respect to prediction result or altogether a different approach.

I am here to talk about something called ensemble modeling and how two types of ensemble techniques would weigh against each other given a problem statement.

Let me just recite the goal of ‘Ensemble Modelling’ from a machine learning engineer’s very friendly neighborhood Python library, Sci-kit Learn aka 'sklearn'. It goes as
‘The goal of ensemble methods is to combine the predictions of several base estimators built with a given learning algorithm in order to improve generalizability/robustness over a single estimator.’

In other words, we are trying to build a powerful model using simple base models in order to achieve better accuracy for a given requirement or problem statement. By ‘base model’, I mean any machine learning algorithm such as Linear regression, Decision Trees, KNN, or any model which acts alone to solve/answer a regression or classification or clustering problem. The process of building such powerful models using base models is called ‘Ensemble modeling’. There are 4 general types of ensemble modeling,

1. Bagging
2. Boosting
3. Stacking
4. Cascading

I am choosing the techniques Bagging and Stacking for discussion. Both are very similar when it comes to the logic that they have been built on but not without key differences. Let us understand both methods first. Hereon, I will be using the phrase ‘base model’ interchangeably with the phrase ‘base estimator’, don’t scratch your head both mean the same thing. The same goes for the terms 'final estimator’ and ’meta-model’.

BAGGING

The word Bagging is acronymized from the statistical phrase ‘Bootstrapped Aggregation’. The method involves aggregating the predictions from base estimators trained on random samples of size m lesser than the original dataset of size n. And below is the schematic representation.



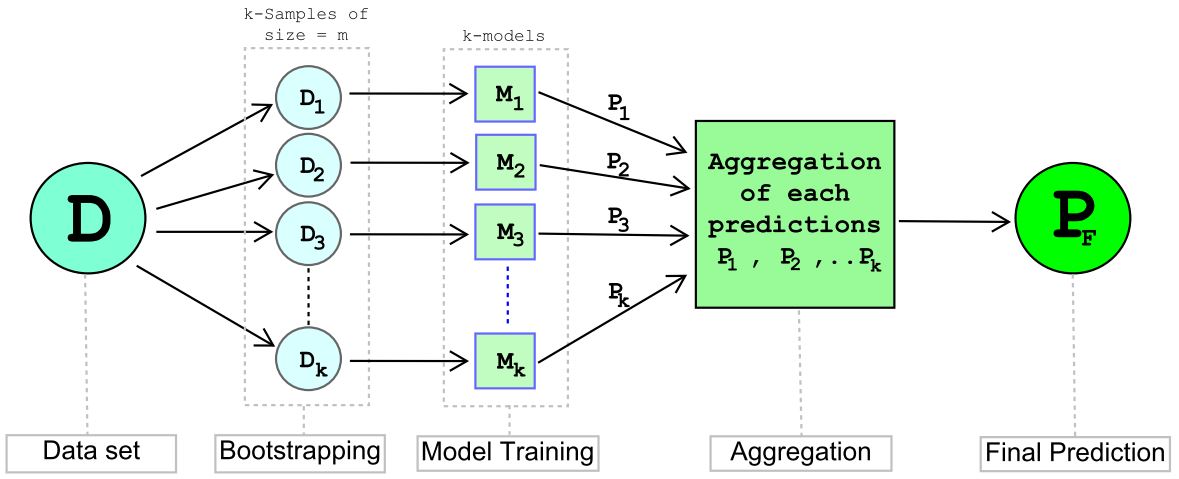
1. Bootstrapping:

It is a statistical technique where we draw k number of random samples, each of size m from the training dataset D={x_i,y_i} of size n such that m ≤ n by replacement. For example, a random sample D₁ of size m is created and will be replaced into dataset D, then the random sample D₂ of size is created and will be replaced into dataset D and so on, we will create k random samples of each size m.

2. Model Training:

We will build low bias-high variance, homogeneous models (overfitting models) M₁, M₂, M₃...M_k to train k-bootstrapped samples. Since each of the models will possibly be trained on an exclusive m-size dataset sampled from the D of size n, we will end up with a low bias-low variance aggregated model, M.

3. Aggregation:

We will have P₁, P₂, P₃...P_k predictions from M₁, M₂, M₃...M_k models which were trained on D₁, D₂, D₃...D_k bootstrapped samples. Aggregation is simply choosing a majority vote as the final prediction P_f amongst k predictions in case the problem statement is ‘Classification’ (or) if the problem statement is ‘Regression’, we will consider either the mean or the median of the k-predictions as the final prediction P_f.

Algorithm code from Sci-Kit Library

For classification: sklearn.ensemble.BaggingClassifier()
For Regression: sklearn.ensemble.BaggingRegressor()

The best example of one of the bagging method applications is the Random Forest algorithm built on low bias-high variance decision trees(Well, this is a topic for another discussion!).

STACKING

Stacking is an ensemble technique that estimates the final estimator or meta-model trained on predictions from multiple base estimators/models using a meta-classifier. The schematic representation of the stacking technique is as below.

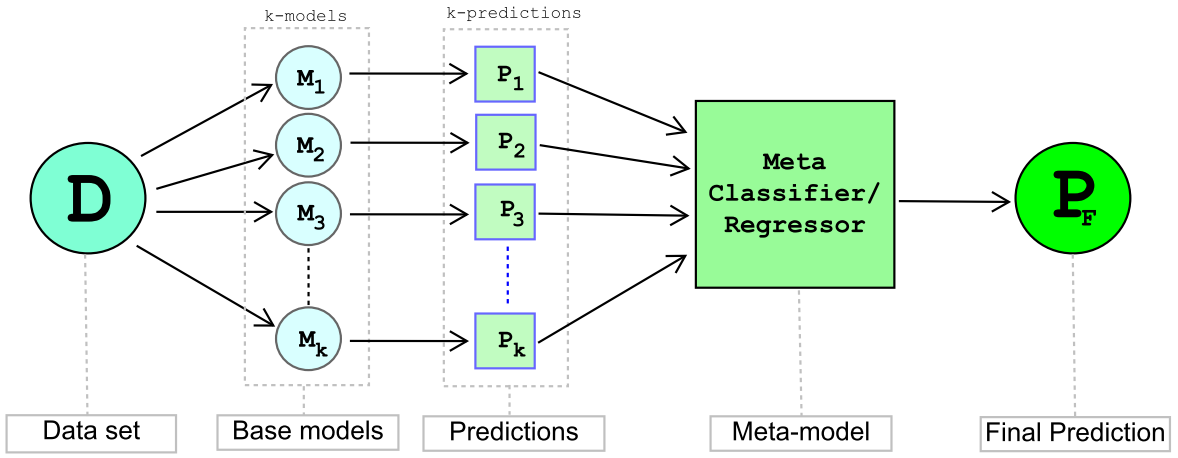
1. Base models are generally heterogeneous i.e., each of the base models will usually be different from one another. For example, given a classification problem, M₁ could be the Decision Tree, M₂ could be the Naïve Bayes classifier, and M₃ could be the KNN classifier and so on.
   

2. Each of the base models will be usually trained on the complete training dataset. Each base model is optimized for the best possible bias-variance trade-off as they are usually trained on the entire dataset. The advantage of randomization can be utilized in the stacking method as well. However, the native implementation of Stacking from the Sci-kit library does not allow any random sampling as a parameter; but, we can use the library mlextend to achieve random sampling.
   

3. A final estimator or meta-model will be used to provide the final prediction. The meta-model is trained on a new dataset D’= {x_i’,y_i} where x_i’ is the prediction from each of the base estimators.
   

Algorithm code from Sci-Kit Library:

For classification: sklearn.ensemble.StackingClassifier()
For Regression: sklearn.ensemble.StackingRegressor()

COMPARISON BETWEEN BAGGING AND STACKING

Although both techniques look highly resembling over a bird's view, there are key differences in the ideology behind each method. Let us dive in to understand the resemblances and the differences.

1. Training Data

The bagging method uses the random samples bootstrapped from the whole training dataset to train the base estimators/models.

The stacking method uses the whole training dataset to train the base estimators/models. However, as mentioned previously, each model can be trained on a random sample from the whole training dataset. But, it’s unlikely to train the base models on the random samples in the stacking technique.

2. Base estimators/models

In the bagging method, base estimators are usually homogeneous i.e., each base model will be the same base estimator. For example, all M₁, M₂, M₃...M_k could be Decision trees for a classification problem.

In the stacking method, base estimators are usually heterogeneous. For example, for a classification problem, M₁ could be a Decision Tree, M₂ could be the Naïve Bayes classifier, M₃ could be the KNN classifier and so on.

3. Final Prediction

In bagging, the final prediction is estimated by a simple aggregation; a majority vote for a classification problem or mean/median for a regression problem. In stacking, the final prediction is the prediction from a meta-model which is trained on the predictions of the base models.

4. Bias-Variance

In bagging, each base model will be a low bias-high variance model. Since each base model is trained exclusively on the bootstrapped sample, the overall bagging model will automatically turn out to be a low bias-low variance model.

In stacking, each base model and the Meta-model is optimized to the best of the bias-variance trade-off. Hence stacking altogether will usually be well optimized in terms of bias-variance trade-off. However, we cannot also defy the possibility of overfitting given the fact that the final prediction is also from a model trained on predictions estimated by base estimators.

5. Training time complexity

Bagging’s training time complexity is just the time complexity of the base model scaled by the number of base models. Hence, it can be represented as O(z*k) time where z is the order of the training time of the base model and k is the number of estimators.

It is not easy to define the time complexity for the stacking method. However, it can be generalized as the summation of the time complexity of each base estimator and the final estimator. It can be represented as O(z₁+z₃...+z_k + Z) time where each z₁, z₂...z_k time complexity of each of the base models and Z is the time complexity of the meta-model.

Hence, time complexity could be relatively higher for the stacking method based on the base models we are using, the number of base models, and the type of meta-model we are using.

6. Space Complexity

Bagging will usually have a space complexity as same as the base estimator but scaled by the number of estimators used. Hence, it can be represented as O(z * k) space where z is the space complexity of the base model and k is the number of base models.

The space complexity for stacking models will be represented as the addition of space complexity of each of the base models and the space complexity of the meta-model i.e., O(z₁+z₃...+z_k + Z) space where each z₁, z₂...z_k are the space complexity of base models and Z is the space complexity of the meta-model.

Hence, space complexity could be relatively higher for the stacking method based on the base models we are using, the number of base models, and the type of meta-model we are using.

7. Parallel computing

Since the base models are independent of one another in both the bagging method and stacking method, parallel computing of base models can be enabled in both methods.

8. Computational cost

The stacking method incurs relatively higher computational cost in comparison with the bagging method given that each base estimator in stacking has to be optimized for the best fit which is followed by the cost of cross-validation and hyper-parameter tuning to do so and the computational cost to train both heterogeneous base models and a meta-model upon that.

In a nutshell, stacking would perform slightly better than bagging on a generalized platform of parameters and dataset size, basically because it involves using a meta-model to estimate final different base estimators. However, it is also associated with higher space complexity, time complexity, and computational cost.

Now, going back to the title question, would you bag your models or rather stack them?

Well, the answer can never be generalized. The quintessential answer to this question is always going to be possibly dependent on any one of the above parameters. It is an unsaid truth that we, machine-learning engineers should never be biased towards any one method or any one algorithm.

To choose an algorithm we should always look at the problem statement, the domain it is from, the data available and then to decide on the model we should compare the performance of each of the method/models with set parameters. Of course, I am well aware that I am being generous in outlining this process. In the real world, this is where we have to scratch our heads a lot. But the bottom line is that there are a lot of processes involved in designing or choosing an algorithm.

Now, to choose between bagging and stacking, consider the difference in performance metrics like accuracy or precision and recall or confusion matrix for the given problem statement. If the problem statement actually requires that minute jump in the performance metric at the cost of time and space complexity and computational cost, then we can choose to stack.

In real-time, stacking is sparsely implemented. Stacking is usually used in Kaggle competitions or only at the organizational levels which handle problem statements that actually aim at getting even that minute performance jump without minding the cost associated.

So, DECIDE based on the analysis of the requirement and not just on the intuitional bias.