K-Fold Cross Validation

In machine learning, we must build a model which predicts the output accurately. The model which we build should also perform well on the unseen data. This is one of the challenges in building an accurate model. To overcome this challenge, we use a technique called Cross-Validation in machine learning.

Cross Validation

Cross validation is used for evaluating machine learning model and testing its performance. Here instead of depending on a single train-test split, it divides the dataset into multiple subsets. These subsets are used to train the model and the process is repeated multiple times with different subsets. In the end, the result from all iterations is averaged and the model performance is measured.

In this method, there is no random splitting, random sampling, or overlapping of the test set. When we just use a train-test split, the samples are randomly picked and if a similar type of dataset is present in the test set with respect to the training set, then the accuracy of the model goes down. Even when we change the random state variable the accuracy will differ.

Basic Steps for Cross validation:

• First, we reserve a subset as the validation set
• Next, train the model using the remaining subsets.
• After training the model, use the validation subset to check the performance
• Repeat the above steps (the number of iterations depends on the type of cross validation we use)

Applications

• Can be used to compare the performance of different models.
• Has great scope in the medical field.

Types of Cross Validation

1. Hold out
2. Leave one out Cross Validation
3. K-folds Cross Validation
4. Stratified K-folds Cross Validation
5. Repeated K-folds Cross Validation
6. Time Series Cross Validation

Leave One Out Cross Validation

It is a type of cross validation in which one sample from the dataset is considered a validation set and the remaining (n-1) samples are considered training sets. This process is repeated for each dataset, that is we get an n-different training set and an n-different test set. The accuracy of the model is average for all n cases.

Example: let us consider a dataset with 5 records

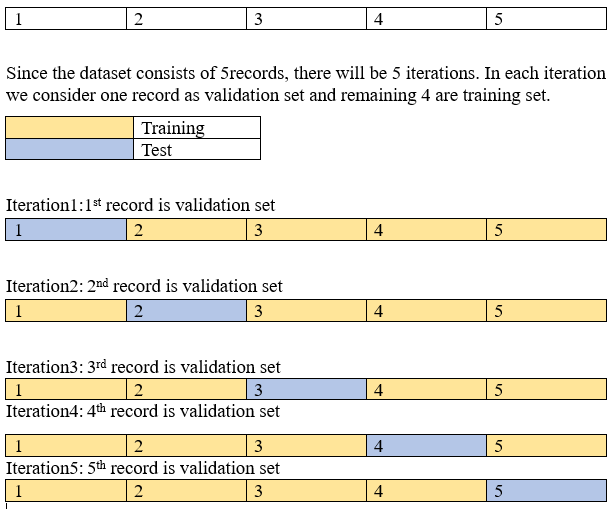
Each iteration gives an accuracy of its own and the accuracy of the model is the average of all the 5-iteration accuracy. Now imagine if the dataset consists of 1000 records, for this it requires 1000 iterations to predict the accuracy of the model. This takes up a lot of computational resources.

In this method the bias is minimum but it requires a lot of computational power and a lot of execution time due to many iterations. It was used in the olden days and in the present we have other better cross validation methods as it is faster.

K-fold Cross validation

The most used method is k-fold cross validation. In the k-fold method instead of taking each sample record as a validation set, we divide the dataset into k number of groups of samples of equal sizes. Then 1 group is considered as the test set and the remaining k-1 set as the training set. The model is trained k-times and ensures every record in the dataset is used for both training and validation. This improves the execution compared to the Leave-one-out method.

Steps for K-fold:

• Split the dataset into k-groups.
• For each group: a) Take one group as a test set b) Remaining k-1 group for training purposes c) Evaluate the performance

Example: Let us consider a dataset with 25 records and divide the dataset into 5 groups of samples(k=5)

The dataset consists of 25 records and is divided into 5 groups; 5 iteration takes place. Now dataset is divided by 5 to get an equal number of records in each group. So, each group has 5 records.

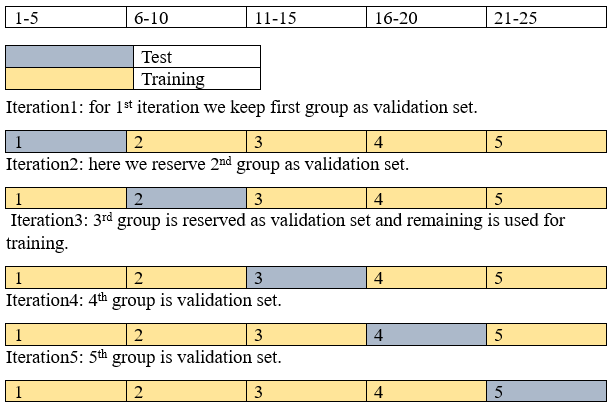
The accuracy is the average of all 5 iterations. This approach helps to avoid overfitting which can occur as the model is trained with all the data and has a lower variance estimate compared to the Holdout method.

Another reason to use this approach as it is useful when the amount of data is limited. This allows us to make better use of available data.

Even this model has drawbacks. For example, consider the dataset used for classification is binary type which consists of 0’s and 1’s, let the 1st group in 1st iteration has only one type of instance as output(0’s), which might become an imbalanced dataset and this may lead to decrease in accuracy. To overcome this drawback, we use Stratified Cross Validation.

It is not to be used for imbalanced datasets and is not suitable for time series data.

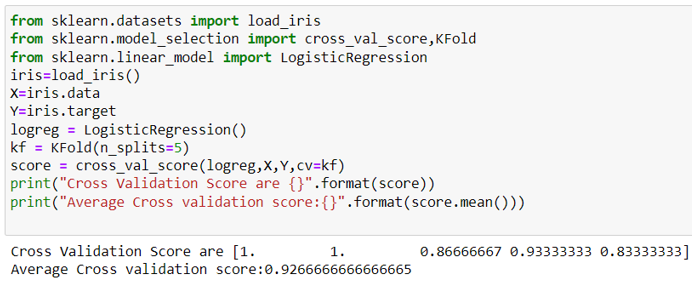
We can import k-fold cross validation from sklearn.model_selection.KFold .

Python Implementation

Conclusion

Cross validation is mainly used to estimate the accuracy of machine learning models on unseen data. Providing a more reliable assessment of model performance and effective utilization of limited data, it helps in building robust and generalizable models. With K-fold cross validation, we can take better decisions about model selection, and hyperparameter tuning and deploy more accurate models in real-world scenarios.