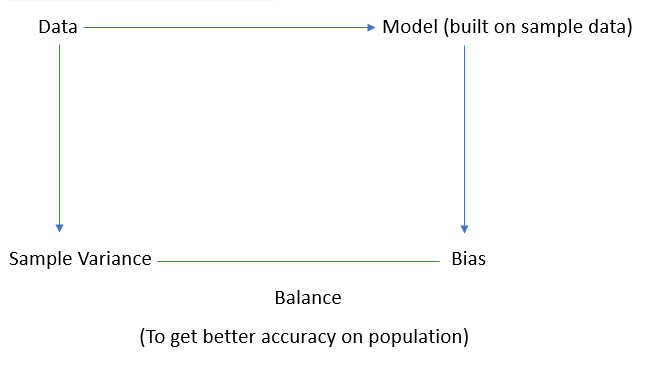
BIAS-VARIANCE TRADE OFF

Consider yourself a farmer attempting to raise crops in your field. Your goal is to produce a large number of healthy plants. You must choose which fertilizers to utilize, how much water to offer, and when to harvest. The weather plays a major element in your success.

If the temperature is too hot or too dry, your plants may not grow properly. On the other side, if the weather is excessively cold or rainy, your crops may be susceptible to disease or pests. The key to success is to strike the perfect balance between providing sufficient care for your plants without overdoing it.

Similarly, in the field of machine learning, we face a similar challenge called the bias-variance tradeoff. Our goal is to build a model that can accurately predict outcomes for new and unseen data

What is Bias?

Bias measures how far off predictions are from actual values. To elaborate, when training on the provided data, the model makes certain assumptions. These assumptions may not always be correct when applied to testing/validation data.

Example:

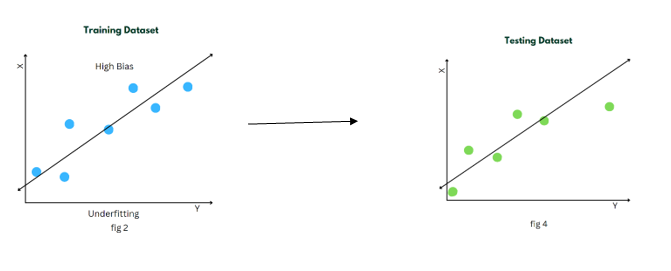
A high-bias model is often too simplistic or limited in its representation of the underlying data. It oversimplifies the relationships between input features and the target variable, resulting in an inability to capture the complexity of the data. This leads to underfitting, where the model fails to learn the underlying patterns and performs poorly not only on the training data but also on new, unseen data.

What is Variance?

In the context of machine learning, variance is closely related to the concept of overfitting. A model with high variance is overly complex and captures noise or random fluctuations in the training data. It tends to fit the training data very closely.

Example:

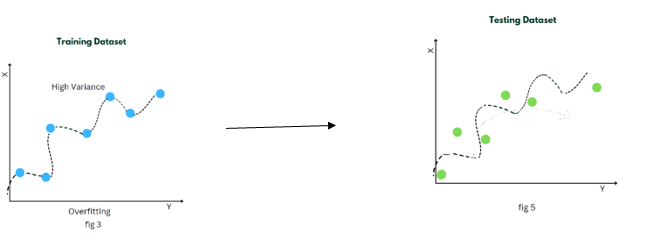
When a model has high variance, it performs well on the training data but fails to generalize to new, unseen data. This is because the model has learned the specific details of the training examples so well that it struggles to make accurate predictions on new data points that may have slightly different characteristics.

High variance can be visualized as a model that has many twists and turns, following each individual data point closely. It tends to have a large number of parameters or features, making it highly flexible and capable of capturing intricate patterns in the training data.

Bias-Variance Tradeoff

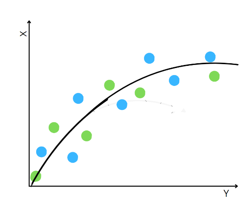
The bias-variance trade-off arises due to the relationship between model complexity, bias, and variance. As the complexity of a model increases, its ability to capture underlying patterns improves, resulting in lower bias. However, with increased complexity, the model becomes more sensitive to noise and fluctuations in the training data, leading to higher variance. Conversely, reducing model complexity decreases its sensitivity to noise, thereby reducing variance, but at the cost of potentially increasing bias. Thus, achieving the right balance involves finding an optimal level of complexity that minimizes both bias and variance.

The goal of machine learning is to find the optimal trade-off between bias and variance, where the model is sufficiently complex to capture the relevant patterns in the data but not overly complex to the extent that it starts capturing noise. This trade-off leads to a model that generalizes well to unseen data and makes accurate predictions.

How to Find the Right Balance Between Bias and Variance?

• Regularization Regularization techniques like Lasso, Ridge regression, and Elastic Net can help us get a model with low bias and low variance.
• Ensemble Methods Ensemble methods like Random Forest, Bagging, and Boosting can help us combine simpler models into a single, more powerful one.